jueves, 15 de noviembre de 2012

movimiento circular uniforme y uniformemente acelerado

El movimiento circular uniformemente acelerado, MCUA, es un caso particular de la velocidad y la aceleración angular, es un movimiento circular cuya aceleración α es constante.
Dada la aceleración angular α podemos obtener el incremento de la velocidad angular ω entre los instantes t₀ y t₁. La ecuación resultante de la velocidad es:

ω (t)=ω₀+α₀(t₁-t₀)

siendo α la aceleración, ω₀ la velocidad inicial, y (t₁-t₀) el incremento de tiempo.
Dada la velocidad angular ω en función del tiempo, podemos hallar la posición θ entre los instantes t₀ y t₁. La ecuación resultante es:

Δθ=ω₀·Δt +½a₀·(Δt)²

siendo a₀ la aceleración, ω₀ la velocidad inicial, y (t₁-t₀) el incremento de tiempo.
Apreciese la similitud con las fórmulas del MRUA, movimiento rectilíneo uniformemente acelerado

se muestra una gráfica de la velocidad angular en función del tiempo, el área en color azul mide el desplazamiento angular total del móvil entre los instantes t₀ y t, el arco en color azul marcado en la circunferencia.

Hallamos la posición angular q del móvil en el instante t, sumando la posición inicial q₀ al desplazamiento, calculado mediante la medida del área bajo la curva w-t o mediante cálculo de la integral definida en la fórmula anterior.

Dada la aceleración angular, hallar el cambio de velocidad angular

Del mismo modo que hemos calculado el desplazamiento angular del móvil entre los instantes t₀ y t, a partir de un registro de la velocidad angular w en función del tiempo t, podemos calcular el cambio de velocidad w -w₀ que experimenta el móvil entre dichos instantes, a partir de una gráfica de la aceleración angular en función del tiempo.

En la figura, el cambio de velocidad w -w₀ es el área bajo la curva a - t, o el valor numérico de la integral definida en la fórmula anterior. Conociendo el cambio de velocidad angular w -w₀, y el valor inicial w₀ en el instante inicial t₀, podemos calcular la velocidad angular w en el instante t.

Resumiendo, las fórmulas empleadas para resolver problemas de movimiento circular son similares a las del movimiento rectilíneo.

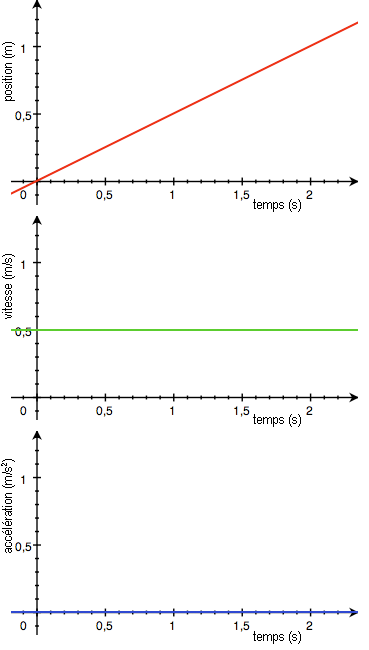
Movimiento circular uniforme

Un movimiento circular uniforme es aquél cuya velocidad angular w es constante, por tanto, la aceleración angular es cero. La posición angular q del móvil en el instante t lo podemos calcular integrando q -q₀=w(t-t₀) o gráficamente, en la representación de w en función de t.

Habitualmente, el instante inicial t₀ se toma como cero. Las ecuaciones del movimiento circular uniforme son análogas a las del movimiento rectilíneo uniforme

Movimiento circular uniformemente acelerado

	Un movimiento circular uniformemente acelerado es aquél cuya aceleración a es constante. Dada la aceleración angular podemos obtener el cambio de velocidad angular w -w₀ entre los instantes t₀ y t, mediante integración, o gráficamente.
	Dada la velocidad angular w en función del tiempo, obtenemos el desplazamiento q -q₀ del móvil entre los instantes t₀ y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando

Habitualmente, el instante inicial t₀ se toma como cero. Las fórmulas del movimiento circular uniformemente acelerado son análogas a las del movimiento rectilíneo uniformemente acelerado.

Despejando el tiempo t en la segunda ecuación y sustituyéndola en la tercera, relacionamos la velocidad angular ω con el desplazamiento θ-θ₀

tiros parabolicos horizontal y oblicuo

Cuando un objeto presenta un movimiento uniforme horizontal y al mismo tiempo presenta un movimiento vertical rectilíneo (suma de movimientos) esto da origen al llamado tiro vertical.

Existen dos tipos de tiro parabólico, está el tiro parabólico horizontal y el tiro parabólico oblicuo, el primero de ellos (tiro parabólico horizontal) es identificado por la forma peculiar en que se comporta el movimiento del cuerpo ya que al lanzar el objeto de forma horizontal al vacio la trayectoria que sigue es de forma curvada, la trayectoria es de esta manera (curva) ya que el cuerpo lanzado es influenciado por dos movimientos, uno de ellos es un movimiento horizontal con una velocidad constante y el otro es de forma vertical.

El tiro parabólico oblicuo se caracteriza porque cuando se lanza un objeto, este forma un ángulo con el eje horizontal, ejemplo, cuando se lanza una bala con un cañón, al llegar la bala al objetivo, esta requiere de cierto ángulo.

En si como se trata de un movimiento de dos dimensiones, el objeto lanzado de esta manera, se moverá en el plano, es decir, se mueve en la direcciones xy (se mueve en dirección al eje x pero simultáneamente se mueve en dirección a eje y).Cuando uno trata con un problema donde se presenta un tiro parabólico horizontal o oblicuo, la persona encargada en darle solución debe tener cuidado en elegir el sistema de coordenadas, ya que, el eje y (la parte positiva) debe de ser vertical y positiva.

La aceleración en el eje y (dirección y) es – g (- 9.80 m/s²) al igual que en la caída libre, mientras que la aceleración en el eje x (dirección x) debe de ser cero debido a que se ignora la resistencia del aire).Cuando el vector de velocidad forma un ángulo con el eje horizontal, a este ángulo se le llama ángulo de proyección (θ₀).

Con las definiciones de seno y el coseno podemos afirmar las siguientes formulas para obtener la velocidad inicial del objeto (velocidad de despegue) en la dirección x y en la dirección y.

Ahora como sabemos que en el tiro vertical sin importar el tipo se presentan dos tipos de movimientos lo más sensato es tratar de separar cada uno de ellos para manejarlos por separado, por suerte se ha comprobado que estos movimientos en si en su naturaleza están separados uno de con el otro, es decir, el movimiento en la dirección x (horizontal) no afecta o influencia en nada al movimiento en la dirección y (vertical).

Comenzaremos por el movimiento en la dirección x, como se menciono anteriormente la aceleración a lo largo de esta dirección será cero (constante), por este motivo el valor inicial del componente de velocidad a lo largo de esta dirección x será contante, es decir, será igual para cada instante de tiempo posterior.

Por lo tanto:

Ahora utilizaremos la ecuación anterior y la sustituimos en la ecuación de la definición de velocidad, eso con el motivo de hallar el desplazamiento del objeto en la dirección x (horizontal) en función del tiempo.

Entonces la formula queda de la siguiente manera:

Con las dos formulas anteriores se nos expresa todo lo necesario de saber sobre el movimiento en la dirección x.

En la dirección y (vertical) como existe una aceleración constante (a =- g), se utilizarán las mismas formulas empleada para el movimiento rectilíneo uniforme acelerado (MRUA), es decir:

Para obtener la rapidez v en cualquier instante se utilizara el teorema de Pitágoras aplicado a los componentes de velocidad, por lo tanto. La formula queda de la siguiente manera:

movimiento en dos dimenciones

Cuando pateas un balón, el balón hace un movimiento en dos dimensiones llamado tiro parabólico.

Se le llama en dos dimensiones, porque la posición de la partícula en cada instante, se puede representar por dos coordenadas, respecto a unos ejes de referencia.

El movimiento en 2 dimensiones es cuando la partícula se mueve tanto horizontal como verticalmente (por así decirlo).
El movimiento de una partícula en dos dimensiones es la trayectoria de la partícula en un plano (vertical, horizontal, o en cualquier otra dirección del plano).Las variables a las que está sometida la partícula son dos y por eso se le denomina movimiento en dos dimensiones.

Movimiento de Proyectiles

Un proyectil es un objeto sobre el cual la única fuerza que actúa sobre él es la gravedad. Hay una variedad de ejemplos de proyectiles: un objeto que se lanza desde un precipicio es un proyectil; un objeto que se lanza verticalmente hacia arriba es también un proyectil; y un objeto es qué lanzado hacia arriba en ángulo también está un proyectil. Todos estos ejemplos se dan con la condición de que la resistencia del aire se considera insignificante.
Un proyectil es cualquier objeto que se proyectara una vez que continúa en el movimiento por su propia inercia y es influenciado solamente por la fuerza hacia abajo de la gravedad.

caida libre y tiro vertical

En estos movimientos el desplazamiento es en una sola dirección que corresponde al eje vertical (eje "Y")

Es un movimiento uniformemente acelerado y la aceleración qu actúa sobre los cuerpos es la de gravedad representada por la letra g.

Sus vaores son.

g=9.81 m/s2 SI. g=981 cm/s2

g=32.16 ft/s2 S. Inglés.

Lo que diferencia a la caida libre del tiro vertical es que el segundo co,prende subida y bajada, mientras que la cida libre unicamente contempla la bajada de los cuerpos.

FÓRMULAS DE CAIDA LIBRE:

Vf= Vo +gt

Vf2= Vo2 +2gh

h= Vo t + g t2 /2

TIPS PARA LA RESOLUCIÓN DE PROBLEMAS DE CAIDA LIBRE:

1.-Un objeto se deja caer......... Vo=0

2.-Se lanza...................... Vo diferente a 0

PROBLEMA:

*Se deja caer una pelota desde la parte alta de un edificion, si tarda 3s en llegar al piso ¿Cuál es la altura del edificio? ¿Con qué velocidad se impacta contra el piso?

h= ? Vf= vO +gt

t= 3s Vf= 0 + (9.81 m/s2)(3s)

Vf= ? Vf=29.43 m/s

Vo= 0m/s

g=-9.81 m/s2 h=vo*t + 1/2 gt2

h=1/2 (9.81m/s2)(3s)2

h=44.14 m

TIRO VERTICAL

Al igual que caida libre es un movimiento uniformemente acelerado.

Diferencia: Forma ascendente y descendente.

Vo diferente a 0 sube:+ baja: -

Al igual que la caida libre es un movimiento sujeto a la aceleración de la gravedad, sólo que ahora la aceleración se opone al movimiento inicial del objeto. El tiro vertical comprende subida, bajada de los cuerpos u objetos considerando lo siguiente:

a)Nunca la velocidad inicial es igual a 0.

b)Cuando el objeto alcanza su altura máxima, su velocidad en este punto es 0. Mientras que el objeto se encuentra se subida el signo de la V es positivo; la V es 0 a su altura máxima cuando comienza a descender su velocidad será negativa

c)Si el objeto tarda por ejmplo 2s en alcanzar su altura máxima tardará 2s en regresar a la posición original, por lo tanto el tiemop que permaneció en el aire el objeto es de 4s.

d)Para la misma posición del lanzamiento la velocidad de subida es igual a la velocidad de bajada.

Fórmulas:

Vf= Vo-gt

Vf2= Vo2 - 2gh

h= Vo * t - 1/2 at2

PROBLEMAS:

*Se lanza verticalmente hacia arriba una pelota con una velocidad inicial de 30 m/s,calcula:

a)Tiempo que tarda en alcanzar su altura max.

b)Altura max.

c) Posición y velocidad de la pelota a los 2s de haberse lanzado

d)V y posición de la pelota a los 5s de haber sido lanzado

e)tiempo que la pelota estuvo en el aire.

Vo= 30m/s t= Vf - Vo / g

t= ? t= 0m/s - 30m/s / 9.81 m/s2

h= ? a) t= 3.058 s

Vf= 0 m/s b)h= Vf2 - Vo2 / -2g

g=-9.81m/s 2 h= 0m/s - 900 m/s / -(2)(9.81 m/s2)

h= 45.87 m

Vf= Vo -gt

Vf= 30m/s - 9.81 m/s2 * 2s

c) Vf= 0.38 m/s h= 40.38m

Vf= 30m,/s - 9.81 m/s2 * 5s

d) Vf= -19.05 m/s h=27.37 m

t= 3.05 s * 2

e) t= 6.10 s

movimiento uniformemente acelerado

En física, el movimiento uniformemente acelerado (MUA) es aquel movimiento en el que la aceleración que experimenta un cuerpo permanece constante (en magnitud y dirección) en el transcurso del tiempo.

El movimiento rectilíneo uniformemente acelerado, en el que la trayectoria es rectilínea, que se presenta cuando la aceleración y la velocidad inicial tienen la misma dirección.
El movimiento parabólico, en el que la trayectoria descrita es una parábola, que se presenta cuando la aceleración y la velocidad inicial no tienen la misma dirección.

En el movimiento circular uniforme, la aceleración tan solo es constante en módulo, pero no lo es en dirección, por ser cada instante perpendicular a la velocidad, estando dirigida hacia el centro de la trayectoria circular (aceleración centrípeta).Por ello, no puede considerarsele un movimiento Movimiento uniformemente acelerado en mecánica clásica
En mecánica clásica el movimiento de una partícula sometida a una fuerza constante resulta ser un movimiento uniformemente acelerado. En el caso más general la trayectoria de una partícula sometida a una fuerza constante resulta ser una parábola.
Para analizar la situación supondremos que se aplica una fuerza constante a una partícula que se mueve inicialmente con velocidad $v_0 \,$ . Sin pérdida de generalidad, podemos suponer que el movimiento se presenta en el plano XY sujeto a las ecuaciones:

$\left \{ \begin{array}{llll} \ddot{x}=0 & \mathrm{con} \quad x(0)=0 & \mathrm{y} \quad \dot{x}(0)=v_{0,x}t\\ \ddot{y}=a_y & \mathrm{con} \quad y(0)=0 & \mathrm{e} \quad \dot{y}(0)=v_{0,y}t \end{array} \right .$

Integrando las ecuaciones diferenciales anteriores se tienen las siguientes velocidades y desplazamientos:

$\left \{ \begin{array}{lll} \dot{x}(t)=v_{0,x} & \Rightarrow & x(t)=v_{0,x}t \\ \dot{y}(t)=v_{0,y}+a_0t & \Rightarrow & y(t)=v_{0,y}t + \cfrac{a_0 t^2}{2} \end{array} \right .$

Para encontrar la ecuación de la trayectoria se despeja el tiempo de la expresión para la coordenadas $\scriptstyle x(t)$ y se substituye $\scriptstyle t(x)$ para obtener $\scriptstyle y(t(x))$ :

$y(x) = \frac{v_{0,y}}{v_{0,x}} + \frac{a_0}{2v_{0,x}^2}x^2$

Movimiento bajo fuerza constante en mecánica relativista
En mecánica relativista no existe un equivalente exacto del movimiento uniformemente acelerado, ya que la aceleración depende de la velocidad y mantener una aceleración constante requeriría una fuerza progresivamente creciente. Además desde el punto de vista de la teoría de la relativdad especial no es realista suponer que pueda existir un cuerpo con aceleración constante indefinidamente ya que tras un tiempo suficientemente largo de aceleración uniforme el cuerpo acabaría teniendo una energía cinética infinita, lo cual no es realista. Para un cuerpo hipotético partiendo del reposo y sometido a la aceleración constante a, ese tiempo es igual a la c/a (c:velocidad de la luz

el movimiento rectilineo uniforme

Movimiento rectilíneo uniforme

El Movimiento Rectilíneo Uniforme es una trayectoria recta, su velocidad es constante y su aceleración es nula.

Un movimiento es rectilíneo cuando el cuerpo describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU.
El MRU (movimiento rectilíneo uniforme) se caracteriza por:

Movimiento que se realiza sobre una línea recta.
Velocidad constante; implica magnitud y dirección constantes.
La magnitud de la velocidad recibe el nombre de aceleridad o rapidez.
Aceleración nula.

sistemas de diferencia absoluto y relativo

Sistemas De Referencia Absoluto Y Relativo

Al hablar de un sistema de referencia simplemente se está apuntando que para observar el movimiento de un objeto es necesario tener un punto de referencia que no proporcione datos reales de distancia, desplazamiento, velocidad, aceleración, etc. Ejemplo; una persona parada observando una carrera de automóviles. Existen dos tipos de sistemas de referencia, está el sistema de referencia absoluta y el sistema de referencia relativa.

Sistema de referencia absoluta.

Se dice como sistema de referencia absoluta cuando se tiene un el punto de referencia fijo, por ejemplo, si tomamos al sol como un punto de referencia, el cual comparáramos con el movimiento de los planeta, en este ejemplo el sol se podría considerar como un sistema de referencia absoluta.

Observe la siguiente imagen para mayor comprensión.

conseptos basicos del movimiento

conceptos basicos de movimiento.

Un movimiento es rectilíneo cuando el móvil describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU.

El MRU (movimiento rectilíneo uniforme) se caracteriza por:

Movimiento que se realiza sobre una línea recta.
Velocidad constante; implica magnitud y dirección constantes.
La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
Aceleración nula.

características

La distancia recorrida se calcula multiplicando la magnitud de la velocidad (celeridad o rapidez) por el tiempo transcurrido. Esta relación también es aplicable si la trayectoria no es rectilínea, con tal que la celeridad o módulo de la velocidad sea constante.
La celeridad puede ser nula (reposo), positiva o negativa. Por lo tanto el movimiento puede considerarse en dos sentidos; una celeridad negativa representa un movimiento en dirección contraria al sentido que convencionalmente hayamos adoptado como positivo.

De acuerdo con la Primera Ley de Newton, toda partícula permanece en reposo o en movimiento rectilíneo uniforme cuando no hay una fuerza neta que actúe sobre el cuerpo. Esta es una situación ideal, ya que siempre existen fuerzas que tienden a alterar el movimiento de las partículas, por lo que en el movimiento rectilíneo uniforme es difícil encontrar la fuerza amplificada.

Caída libre

Caída libre de una pelota. Se muestra, mediante fotografía estroboscópica, la posiciones de la pelota a intervalos regulares de tiempo.

En mecánica, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Aunque esta definición formal excluye la influencia de otras fuerzas, como la resistencia aerodinámica, frecuentemente éstas deben ser tenidas en cuenta cuando el fenómeno tiene lugar en el seno de un fluido, como el aire o cualquier otro fluido.
El concepto es aplicable incluso a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad o a un satélite (no propulsado) en órbita alrededor de la Tierra.
Otros sucesos referidos también como caída libre lo constituyen la trayectoria geodésica en el espacio-tiempo descrita en la teoría de la relatividad general.

Ejemplos de caída libre (deporte) los encontramos en actividades deportivas^[1] ^[2] tales como dejarse caer una persona a través de la atmósfera sin sustentación aeronáutica o sin paracaídas desplegado.

La caída libre como sistema de referencia [editar]

Un sistema de referencia ligado a un cuerpo en caída libre puede considerarse inercial o no inercial en función del marco teórico que esté utilizándose.
En la física clásica, la fuerza gravitatoria que se ejerce sobre una masa es proporcional a la intensidad del campo gravitatorio en la posición espacial donde se encuentre dicha masa. La constante de proporcionalidad es precisamente el valor de la masa inercial del cuerpo, tal y como establece el principio de equivalencia. En la física relativista, la gravedad es el efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una fuerza, sino una geodésica. Por tanto, desde el punto de vista de la física clásica, un sistema de referencia en caída libre es un sistema acelerado por la fuerza de la gravedad y, como tal, es no inercial. Por el contrario, desde el punto de vista de la física relativista, el mismo sistema de referencia es inercial, pues aunque está acelerado en el espacio, no está acelerado en el espacio-tiempo. La diferencia radica en la propia definición de los conceptos geométricos y cinemáticos, que para cada marco teórico son completamente diferentes.

Caída libre ideal [editar]

Animación de la caída libre.

En la caída libre propiamente dicha o ideal, se desprecia la resistencia aerodinámica que presenta el aire al movimiento del cuerpo, analizando lo que pasaría en el vacío. En esas condiciones, la aceleración que adquiriría el cuerpo sería debida exclusivamente a la gravedad, siendo independiente de su masa; por ejemplo, si dejáramos caer una bala de cañón y una pluma en el vacío, ambos adquirirían la misma aceleración, $g\,$ , que es la aceleración de la gravedad y por tanto, caerían al mismo tiempo.
Por el contrario, cuando la caída tiene lugar en el seno de un fluido (como el aire), hay que considerar la resistencia aerodinámica que actúa sobre el cuerpo. Aunque técnicamente ya no es libre, esta caída se describe matemáticamente con las mismas ecuaciones del movimiento de caída libre, pero agregando el término aerodinámico correspondiente.

Ecuación del movimiento [editar]

Por la segunda ley de Newton, la fuerza $\mathbf{F}$ que actúa sobre un cuerpo es igual al producto de su masa $m\,$ por la aceleración que adquiere. En caída libre sólo intervienen el peso $\mathbf{P}$ (vertical, hacia abajo) y el rozamiento aerodinámico $\mathbf{f}(v)$ en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:

$\mathbf{F} = \mathbf{P}+\mathbf{f} = -mg {\mathbf{j}} - f\frac{\mathbf{v}}{v} = m\frac{d\mathbf{v}}{dt}$

La aceleración de la gravedad $g\,$ lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.

Trayectoria en caída libre [editar]

Caída libre totalmente vertical [editar]

El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleración g) (aproximadamente porque la aceleración aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:

(1) $-mg + f = ma_y \,$

donde:

$a_y, v_y\;$ , son la aceleración y la velocidad verticales.

$f\;$ , es la fuerza de rozamiento fluidodinámico (que aumenta con la velocidad).

Si, en primera aproximación, se desprecia la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan velocidades moderadas, la solución de la ecuación diferencial (1) para las velocidades y la altura vienen dada por:

$\begin{matrix} v_y(t)= v_0 - gt \\ y(t) = h_0 + v_0t -\frac{1}{2}gt^2 \end{matrix}$

donde v₀ es la velocidad inicial, para una caída desde el reposo v₀ = 0 y h₀ es la altura inicial de caída.

Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la resistencia fluidodinámica que suele ser modelizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico k_w:

(2) $-mg - k_wv_y = ma_y \,$

En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial (2):

$\begin{cases} v_y = v_0e^{-k_wt/m} + \cfrac{mg}{k_w}(e^{-k_wt/m}-1) \\ y = h_0 - \cfrac{mgt}{k_w}+m\left(\cfrac{mg+k_wv_0}{k_w^2}\right)(e^{-k_wt/m}-1) \end{cases}$

Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:

$v_\infty = \lim_{t\to \infty} v_y(t) = -\frac{mg}{k_w}$

Un análisis más cuidadoso de la fricción de un fluido revelaría que a grandes velocidades el flujo alrededor de un objeto no puede considerarse laminar, sino turbulento y se producen remolinos alrededor del objeto que cae de tal manera que la fuerza de fricción se vuelve proporcional al cuadrado de la velocidad: (3) $ma_y = m\frac{d^2y}{dt^2} = -mg - \epsilon\frac{C_d}{2}\rho A_tv_y^2$